TIPI DI QUADRANTI SOLARI
I QUADRANTI SU SUPERFICI PIANE
Prima
di dedicarci ai quadranti su superfici piane, riteniamo utile fare
qualche cenno
su un aspetto della geometria che ha particolare importanza nel campo
dei
quadranti solari e che riguarda il modo con il quale piani e superfici
geometriche regolari si intersecano fra di loro nello spazio. In
particolare
ricordiamo che:
-
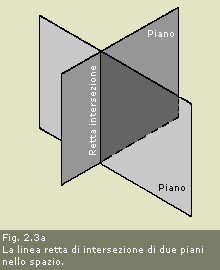 Due piani qualsiasi,
a meno che non siano paralleli fra di loro, si intersecano nello spazio
secondo una retta o, in altre parole, i punti che hanno in comune
risultano allineati fra di loro (vedi la fig. 2.3a).
-
Un cono, con superficie laterale
indefinita, e un piano si intersecano nello spazio secondo curve dette
“coniche” che assumono forme diverse (circonferenze, ellissi, parabole,
iperboli) a seconda delle diverse posizioni reciproche del cono e del
piano.
Il
caso che interessa di più la gnomonica, per le intersezioni fra coni e
piani,
almeno alle nostre latitudini, è illustrato nella fig. 2.3b. In esso si
ipotizza che il Sole percorra nel cielo, per esempio nel giorno del
solstizio
d’estate il suo grande usuale percorso 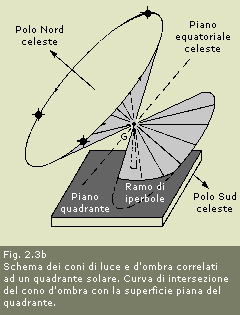 circolare,
congiungendo i punti del
quale con il punto gnomonico G del quadrante si ottiene un grande cono,
molto
aperto, formato dai suoi raggi luminosi. Al di là del punto gnomonico
verso la
superficie del quadro, si forma quindi un altro cono, questa volta
formato da
“raggi d’ombra”, rovesciato rispetto al primo e con la sua stessa
apertura, ma molto più piccolo e che interseca il piano del quadrante
secondo
una curva, della famiglia delle coniche vista sopra, e in particolare
delle
iperboli. Lo stesso discorso vale naturalmente in tutti i giorni
dell’anno con
la sola differenza che, mano a mano che ci si sposta dai giorni dei
solstizi a
quelli degli equinozi, i coni di luce e d’ombra diventano sempre più
aperti e
le iperboli perdono gradualmente la loro curvatura diventando sempre
più
piatte.
Nel
caso particolare dei giorni degli equinozi, quando il percorso del Sole
giace
nel piano equatoriale, il cono si trasforma in un piano e la linea
diurna di
quei giorni (intersezione del piano dell’equatore che passa per il
punto gnomonico con quello del quadrante) diventa una retta, detta
retta equinoziale.
Inoltre
va naturalmente sempre tenuto presente che la distanza effettiva fra il
centro
della Terra e un qualsiasi punto gnomonico posto sulla sua superficie,
è del
tutto trascurabile rispetto alla distanza della Terra dal Sole;
pertanto tutti i ragionamenti di cui sopra, applicabili a rigore solo
al
centro della Terra, possono essere estesi anche a detto punto
gnomonico. In
altre parole ciò equivale a dire che, in prima approssimazione, i raggi
del
Sole giungono su tutti i punti della Terra sempre paralleli fra di loro.
|
TIPI DI
QUADRANTI SOLARI
Generalità
I quadranti a emisfera
I quadranti su superfici piane
I quadranti equatoriali
I quadranti su superfici orizzontali
I quadranti su superfici verticali
I quadranti di altro tipo
Le correzioni e indicazioni accessorie
|